Intro to Principal Component Analysis

Statistics deals with finding order out of chaos. Sometimes, estimating variables is easy Oftentimes we find ourselves with more data than we know what to do with it. With more variables, more information. However, with more variables, there is also exponentially more complexity. This is called the curse of dimensionality. In order to avoid this fate, we use techniques for dimensionality reduction. That is, reducing the amount of variables down to just the most important ones. The techniques for achieving this fall under the umbrella of what is termed Spectral Theory. Spooky, but not so cursed.

Spectral Theory

Wikipedia:

In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces.

Principal Component Analysis

From Fritz’ Blog

Principal component analysis (PCA) is an algorithm that uses a statistical procedure to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components. […] This is one of the primary methods for performing dimensionality reduction — this reduction ensures that the new dimension maintains the original variance in the data as best it can. […] That way we can visualize high-dimensional data in 2D or 3D, or use it in a machine learning algorithm for faster training and inference.

They also lay out the steps for performing PCA.

1. Standardize (or normalize) the data.
2. Calculate the covariance matrix from this standardized data (with dimension d).
3. Obtain the Eigenvectors and Eigenvalues from the newly-calculated covariance matrix.
4. Sort the Eigenvalues in descending order, and choose the 𝑘 Eigenvectors that correspond to the 𝑘 largest Eigenvalues — where 𝑘 is the number of dimensions in the new feature subspace (𝑘≤𝑑).
5. Construct the projection matrix 𝑊 from the 𝑘 selected Eigenvectors.
6. Transform the original dataset 𝑋 by simple multiplication in 𝑊 to obtain a 𝑘-dimensional feature subspace 𝑌.
7. (optional) Calculate the explained variance: how much variance is captured by the PCA algorithm. Higher value = better.

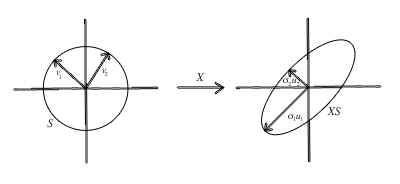
PCA has its own limitations. Mainly, that it involves multiplying all of the samples with each other (which is very cursed) and it doesn’t work so well with non-linear correlations. Luckily, you can always apply your own kernel methods for translating polynomial relationships down to linear problems, but that’s a horror story for another time. There is a more general approach for dimensionality reduction which is also more computationally efficient called Singular value Decomposition, which I’ll write about later. For a step-by-step implementation of PCA in python, check out Nikita Kozodoi’s.

Here I’m using bitanath’s javascript implementation for getting the principal components of a matrix.